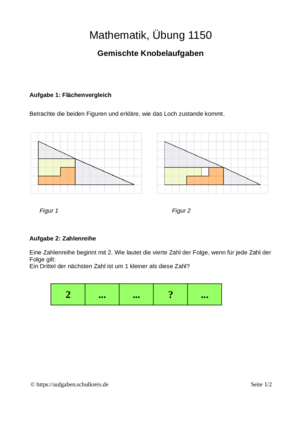
Knobelaufgaben: Sechs interessante Knobelaufgaben sind zu lösen: Zahlenreihe, Logikrätsel, Würfelgebäude, Quadernetz und Zahlenstrahl. Die Aufgaben sind eher leicht zu lösen.
Knobelaufgaben: Sechs Knobelaufgaben sind zu lösen: Teilung eines Kreises, Melonenrätsel (Prozentrechnung), Logikaufgabe, Hundetreffen (Gleichungssystem), Denksportaufgabe und Zahlenreihe. Die Aufgaben sind vom Typ " ... mehr
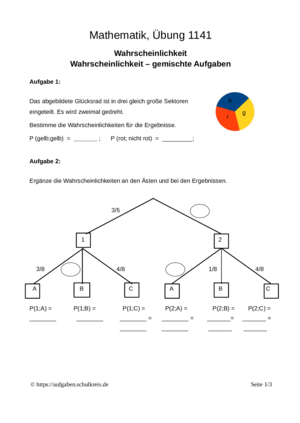
Wahrscheinlichkeitsrechnung, Permutation: In den gemischten Aufgaben zur Wahrscheinlichkeitsrechnung wird der gesamte Bereich abgedeckt. Für die Bearbeitung der acht Aufgaben ist das Beherrschen von Formeln ebenso g ... mehr
Knobelaufgaben: Sechs interessante Denksportaufgaben: Verwandtschaftsverhältnis, Holzwurm im Würfel, Zahlenfolge, parallele Linien, Entfernungsaufgabe, Würfeloberfläche. Die Aufgaben sinf zum Teil schwer zu lösen.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte von zwei Parabeln.
Wahrscheinlichkeitsrechnung: Inhalt der Übung sind Berechnungen mehrstufiger Zufallsexperimente: Mehrmaliges Drehen eines Glücksrades und Ziehen von farbigen Kugeln aus Urnen und Lostrommeln stehen im Mittelpunkt der Aufg ... mehr
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Scheitelpunktform und Normalform einer Parabel.
Wahrscheinlichkeitsrechnung: Es geht um das Berechnen mehrstufiger Zufallsexperimente (Grundwissen). Aufgaben zu mehrfachem Münzwurf, mehrmaligem Drehen eines Glücksrades und Ziehen von mehreren Kugeln aus Urnen sind zu l ... mehr
Wahrscheinlichkeitsrechnung, Permutation: Im Mittelpunkt steht die Permutation. Es sollten die benötigten Kombinatorik-Formeln (Fakultät, n über k) beherrscht werden, um die Vertauschungsmöglichkeiten in den zahl ... mehr
Quadratische Funktionen: Schwerpunkte dieser Schulaufgabe über die quadratischen Funktionen: Normalparabeln zeichnen, Koordinaten des Scheitelpunkts berechnen, Schnittpunkte von Parabeln (auch mit Geraden), Nullstelle bere ... mehr
Gleichungssysteme: 8 Aufgaben zu linearen Gleichungssystemen: Additions- und Subtraktionsverfahren, Einsetzverfahren, Gleichsetzungsverfahren, zeichnerische und rechnerische Lösung werden verlangt.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte einer Parabel mit den Achsen.
Satz des Pythagoras: Vier zum Teil anspruchsvolle Übungsaufgaben zum rechtwinkligen Dreieck (Satz des Pythagoras). Dessen Anwendung soll anhand geeigneter Zerlegungen von Kreis, Rechteck und Trapez geübt werden.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Verschieben der Normalparabel.
Gleichungssysteme: Sechs Übungsaufgaben zu den linearen Gleichungssystemen. Schwerpunkte sind die drei Lösungsverfahren, die rechnerische und zeichnerische Lösung sowie die Anwendung von Gleichungssystemen in Textaufgabe ... mehr
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Erstellen der Parabelgleichung aus gegebenen Punkten.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte einer Parabel mit einer Geraden.
Gleichungssysteme: Acht Übungsaufgaben zu den linearen Gleichungssystemen. Schwerpunkte sind rechnerisches und zeichnerisches Lösungsverfahren und die Anwendung von Gleichungssystemen in Textaufgaben.
Gleichungssysteme: Sieben Übungsaufgaben zu den linearen Gleichungssystemen. Schwerpunkte sind das rechnerische Lösungsverfahren, die Lage von Geraden beim zeichnerischen Verfahren sowie die Anwendung von Gleichungssystem ... mehr
Quadratische Funktionen: Schwerpunkte: Normalparabeln; Ermitteln der Funktionsgleichung; Zeichnen von Parabeln; Scheitelpunktsform und Normalform; Berechnung der Nullstellen; Berechnung der Schnittpunkte zweier Parabeln; Sc ... mehr
Binomische Formeln: Quadratische Gleichungen sollen unter Verwendung der binomischen Formeln umgeformt werden.
Quadratische Ergänzung: Bestimmen Sie die Lösung(en) der quadratischen Gleichungen mit Hilfe der quadratischen Ergänzung.
Quadratische Gleichungen: Bestimmen Sie die Lösungen der quadratischen Gleichungen mit Hilfe der allgemeinen Lösungsformel.
Quadratische Ergänzung: Bestimmen Sie die Lösung(en) der quadratischen Gleichungen mit Hilfe der quadratischen Ergänzung.
Quadratische Gleichungen: Bestimmen Sie die Lösungen der quadratischen Gleichungen mit Hilfe der allgemeinen Lösungsformel.
