Lineare Funktionen: Dies ist Teil 1 der Übungsreihe "Lineare Funktionen". Inhalte: * Wichtige Begriffe zu linearen Funktionen * Wertetabellen
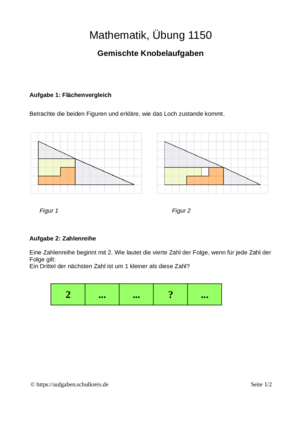
Knobelaufgaben: Sechs interessante Knobelaufgaben sind zu lösen: Zahlenreihe, Logikrätsel, Würfelgebäude, Quadernetz und Zahlenstrahl. Die Aufgaben sind eher leicht zu lösen.
Multiplizieren, Dividieren, Addieren, Subtrahieren, Terme: Es werden Grundlagen der Vereinfachung von Termen verlangt, um die Aufgaben lösen zu können: Terme sollen zusammengefasst, ausmultipli ... mehr
Lineare Funktionen: Dies ist Teil 2 der Übungsreihe "Lineare Funktionen". Inhalte: * Bestimmen von Funktionsgleichungen durch Ablesen von Graphen * Zeichnen von Geraden in Koordinatensysteme * Steigungsdreieck ... mehr
Knobelaufgaben: Sechs Knobelaufgaben sind zu lösen: Teilung eines Kreises, Melonenrätsel (Prozentrechnung), Logikaufgabe, Hundetreffen (Gleichungssystem), Denksportaufgabe und Zahlenreihe. Die Aufgaben sind vom Typ " ... mehr
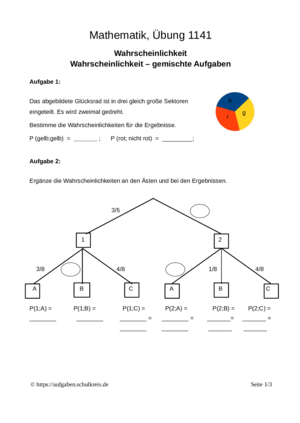
Wahrscheinlichkeitsrechnung, Permutation: In den gemischten Aufgaben zur Wahrscheinlichkeitsrechnung wird der gesamte Bereich abgedeckt. Für die Bearbeitung der acht Aufgaben ist das Beherrschen von Formeln ebenso g ... mehr
Knobelaufgaben: Sechs interessante Denksportaufgaben: Verwandtschaftsverhältnis, Holzwurm im Würfel, Zahlenfolge, parallele Linien, Entfernungsaufgabe, Würfeloberfläche. Die Aufgaben sinf zum Teil schwer zu lösen.
Lineare Funktionen: Dies ist Teil 9 der Übungsreihe "Lineare Funktionen". Inhalte: * Zusammenfassende Aufgaben, der gesamte Bereich der linearen Funktionen sollte zum Lösen beherrscht werden.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte von zwei Parabeln.
Terme: Es geht um Terme und Termumformungen. Schwerpunkte: Zusammenfassen von Ausdrücken, Ausmultiplizieren, Vereinfachen und Umformen in Klammerausdrücke.
Lineare Funktionen: Dies ist Teil 3 der Übungsreihe "Lineare Funktionen". Inhalte: * Bestimmen von Funktionsgleichungen linearer Funktionen bei gegebenem Steigungsfaktor und y-Abschnitt * Abstand zweier Punkte ... mehr
Wahrscheinlichkeitsrechnung: Inhalt der Übung sind Berechnungen mehrstufiger Zufallsexperimente: Mehrmaliges Drehen eines Glücksrades und Ziehen von farbigen Kugeln aus Urnen und Lostrommeln stehen im Mittelpunkt der Aufg ... mehr
Lineare Funktionen: Dies ist Teil 5 der Übungsreihe "Lineare Funktionen". Inhalte: * Ermitteln der Funktionsgleichung aus zwei gegebenen Punkten * Überprüfung der Lage von Punkten * Koordinaten von Punkten b ... mehr
Binomische Formeln: Schwerpunkt sind die binomischen Formeln. Gleichungen sowie Platzhalteraufgaben sind durch Anwendung der binomischen Formeln zu lösen.
Lineare Funktionen: Dies ist Teil 4 der Übungsreihe "Lineare Funktionen". Inhalte: * Ermitteln der Funktionsgleichung linearer Funktionen bei gegebenem Steigungsfaktor und einem Punkt auf der Geraden * Ermitte ... mehr
Lineare Funktionen: Dies ist Teil 6 der Übungsreihe "Lineare Funktionen". Inhalte: * Berechnen des Schnittpunktes zweier Geraden * Berechnen der Nullstelle
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Scheitelpunktform und Normalform einer Parabel.
Wahrscheinlichkeitsrechnung, Permutation: Im Mittelpunkt steht die Permutation. Es sollten die benötigten Kombinatorik-Formeln (Fakultät, n über k) beherrscht werden, um die Vertauschungsmöglichkeiten in den zahl ... mehr
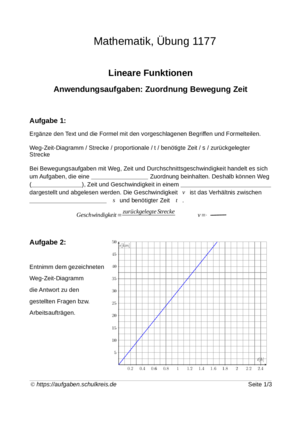
Lineare Funktionen: Dies ist Teil 8 der Übungsreihe "Lineare Funktionen". Inhalte: * Anwendungsaufgaben * Weg-Zeit-Diagramm * Weg, Strecke, Geschwindigkeit
Lineare Funktionen: Dies ist Teil 7 der Übungsreihe "Lineare Funktionen". Inhalte: * Spiegelung an x- und y-Achse * Bestimmen von Funktionsgleichungen * Berechnen von Senkrechten und Nullstellen
Quadratische Funktionen: Schwerpunkte dieser Schulaufgabe über die quadratischen Funktionen: Normalparabeln zeichnen, Koordinaten des Scheitelpunkts berechnen, Schnittpunkte von Parabeln (auch mit Geraden), Nullstelle bere ... mehr
Lineare Funktionen: Schwerpunkte: Funktionsgleichung bei zwei gegebenen Punkten bestimmen; Nullstelle berechnen; Spiegelung an der x-Achse; Umformen von Funktionsgleichungen in die Normalform; Überprüfen, ob ein Punkt auf ... mehr
Gleichungssysteme: 8 Aufgaben zu linearen Gleichungssystemen: Additions- und Subtraktionsverfahren, Einsetzverfahren, Gleichsetzungsverfahren, zeichnerische und rechnerische Lösung werden verlangt.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte einer Parabel mit den Achsen.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Verschieben der Normalparabel.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Erstellen der Parabelgleichung aus gegebenen Punkten.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte einer Parabel mit einer Geraden.
Funktionsgraphen, Lineare Funktionen: In dieser Übung sind zahlreiche Funktionsgraphen zu zeichnen. Dabei soll die Beschriftung der vorgegebenen Koordinatensysteme selbst vorgenommen werden. Die Graphen der linearen ... mehr
Quadratische Funktionen: Schwerpunkte: Normalparabeln; Ermitteln der Funktionsgleichung; Zeichnen von Parabeln; Scheitelpunktsform und Normalform; Berechnung der Nullstellen; Berechnung der Schnittpunkte zweier Parabeln; Sc ... mehr
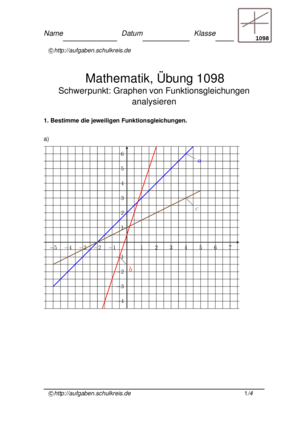
Funktionsgraphen, Lineare Funktionen: Funktionsgleichungen sollen durch Analyse von Graphen ermittelt werden. Die linearen Funktionen sollten gut beherrscht werden, um auch eine Senkrechte zu einer gegebenen Geradeng ... mehr
Lineare Funktionen: Schwerpunkte dieser Übung: Funktionsgleichung bei zwei gegebenen Punkten bestimmen; Senkrechte zu einer Geraden bestimmen; Schnittpunkt zweier Geraden berechnen; Nullstelle berechnen; Überprüfen, ob e ... mehr
Lineare Funktionen: Schwerpunkte: Geraden durch den Ursprung (Normalform: y=mx); Überprüfen, ob ein Punkt auf einer Geraden liegt; Berechnung des Abstandes zweier Punkte; Fehlende Koordinaten bestimmen; Senkrechte zeichne ... mehr
Binomische Formeln: Quadratische Gleichungen sollen unter Verwendung der binomischen Formeln umgeformt werden.
Quadratische Ergänzung: Bestimmen Sie die Lösung(en) der quadratischen Gleichungen mit Hilfe der quadratischen Ergänzung.
Quadratische Ergänzung: Bestimmen Sie die Lösung(en) der quadratischen Gleichungen mit Hilfe der quadratischen Ergänzung.
