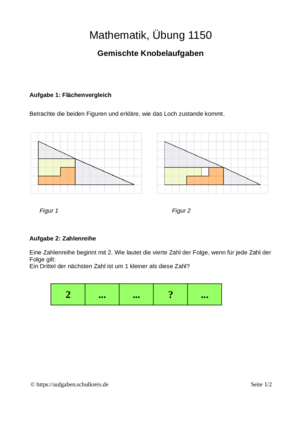
Knobelaufgaben: Sechs interessante Knobelaufgaben sind zu lösen: Zahlenreihe, Logikrätsel, Würfelgebäude, Quadernetz und Zahlenstrahl. Die Aufgaben sind eher leicht zu lösen.
Knobelaufgaben: Sechs Knobelaufgaben sind zu lösen: Teilung eines Kreises, Melonenrätsel (Prozentrechnung), Logikaufgabe, Hundetreffen (Gleichungssystem), Denksportaufgabe und Zahlenreihe. Die Aufgaben sind vom Typ " ... mehr
Knobelaufgaben: Sechs interessante Denksportaufgaben: Verwandtschaftsverhältnis, Holzwurm im Würfel, Zahlenfolge, parallele Linien, Entfernungsaufgabe, Würfeloberfläche. Die Aufgaben sinf zum Teil schwer zu lösen.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte von zwei Parabeln.
Binomische Formeln: Schwerpunkt sind die binomischen Formeln. Gleichungen sowie Platzhalteraufgaben sind durch Anwendung der binomischen Formeln zu lösen.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Scheitelpunktform und Normalform einer Parabel.
Quadratische Funktionen: Schwerpunkte dieser Schulaufgabe über die quadratischen Funktionen: Normalparabeln zeichnen, Koordinaten des Scheitelpunkts berechnen, Schnittpunkte von Parabeln (auch mit Geraden), Nullstelle bere ... mehr
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte einer Parabel mit den Achsen.
Satz des Pythagoras: Vier zum Teil anspruchsvolle Übungsaufgaben zum rechtwinkligen Dreieck (Satz des Pythagoras). Dessen Anwendung soll anhand geeigneter Zerlegungen von Kreis, Rechteck und Trapez geübt werden.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Verschieben der Normalparabel.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Erstellen der Parabelgleichung aus gegebenen Punkten.
Quadratische Funktionen: Übung zu den quadratischen Funktionen: Schnittpunkte einer Parabel mit einer Geraden.
Quadratische Funktionen: Schwerpunkte: Normalparabeln; Ermitteln der Funktionsgleichung; Zeichnen von Parabeln; Scheitelpunktsform und Normalform; Berechnung der Nullstellen; Berechnung der Schnittpunkte zweier Parabeln; Sc ... mehr
